Check out Janggi (Korean Chess), our featured variant for December, 2024.
Check out Janggi (Korean Chess), our featured variant for December, 2024.
Stefanos Pantazis, editor of The US Problem Bulletin, has sent me two problems that appeared in that journal and did win a prize there.
This is the second problem: You can also look at the first problem: a series selfmate in 17 moves.
This problem was composed by Michel Caillaud, was published in the US Problem Bulletin in 1994, and won a First Prize.
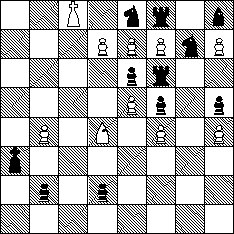White:
King c8; Bishop d4; Pawn b4, d7, e5, e7, f4, f7, h4, h7.
Black:
King a3; Rook f6, f8; Knight e8, g7; Bishop h8; Pawn b2, d2, e6, f5, h5.
Circe. h=4: Helpstalemate in four moves.
(b) Move the black king from a3 to a4, and solve the problem again.
Circe is, as Stefanos Pantazis wrote me, probably the most popular fairy condition among problemists; Circe Chess is also occasionally played as a game between two players, but not too often. In Circe a unit that is captured is immediately reborn on its array square: the square where it stood on the opening setup. A rook, bishop, or knight is reborn on a square of the same colour as the square on which it was captured; a pawn on a square (in the 2nd or 7th rank) in the same file on which it was taken. When the square is occupied, the piece disappears.
A helpstalemate in four moves means: black moves first, and helps white to get himself stalemated. So, what you should find is one series of eight moves, starting with a black move, then a white move, etc., ending with a white move that gives stalemate to black: black cannot move from the resulted position, and is not in check. Note that black and white actually cooperate to get black stalemated.
The problem consists actually of two parts: the problem as stated, and the problem where the black king is moved from a3 to a4. For this second position, the same condition again holds: give a sequence of 4 turns, starting with black, and ending with white stalemating black.
The problem couldn't be computer tested, and the possibility of a cook (additional solution, shorter solution, ...) cannot be ruled out completely, but seems not too likely. Any reader finding such a cook is requested to contact me.