8x8 HYPERBOLIC CHESS
I designed 8x8 hyperbolic chess as follows:
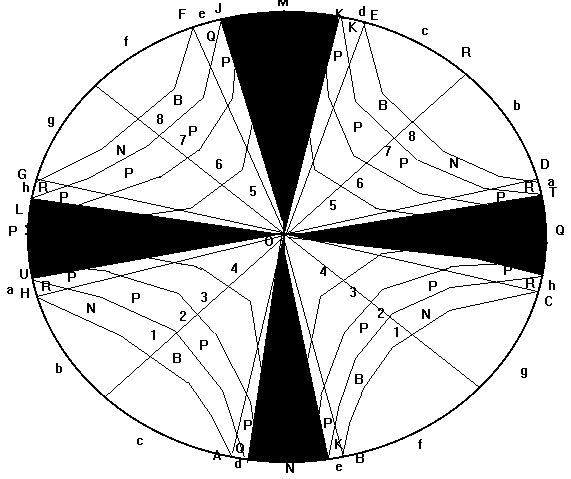
First draw a great circle (C) with center O and two perpendicular diameters MN, PQ which will form the axes 0xy of the hyperbola. Then draw branches of the hyperbola which intersect the great (or the fixed) circle (C) at the curves AB, CD, EF and GH. Then draw the diameters EA, FB, RS, CG, DH , RS, and TI. The result is an 8x8 hyperbolic chessboard. The initial arrangement of pieces as well as the board itself are illustrated on below. The pieces move and capture like the usual 8x8 square chess, except that the frontier between the two opponents is the center O through which all pieces must cross in order to reach the enemy side. The hatched zones cannot be crossed by the pieces. The pieces move along their files identified by the coordinate (x,y) where x=a,b,c,d,e,f,g,h and y=1,2,3,4,5,6,7,8,9. There are two types of cells (the equivalents of the squares): hyperbolic cells formed by the intersections of two radii and two branches of the hyperbola, and hyperbolic triangles formed by the intersection of two radii with one branch of the hyperbola.
One peculiarity of hyperbolic chess is that the diagonal moves of the queen and the bishop are limited to the sectors UOV, WOZ, TOK and JOL. Example: a white queen on d1 cannot diagonally cross the zone VOW and move to the sector WOZ. However, it can diagonally move (for example) from d1 to c2 or b3 or a4.
The other peculiarity of hyperbolic chess, is that the pieces
moving along the rows 1, 2, 3, 8, 7, 6 move like points on the hyperbola branches, which can tend to infinity when we approach the center O of the fixed circle (C). So, pieces move to infinity and return from infinity.
Example: a white Rook on a1 moves to d1, then goes to infinity, then returns from infinity and goes to e1, then moves to g1. So, the zone VOW is a barrier.
Written by A. MISSOUM. Edited by David Howe.
WWW page created: June 30, 1997.
