Spherical Chess
Introduction

From time to time, attempts have been made to translate Chess to a spherical board. Some people have been inspired to build spherical boards and figure out how to play Chess on them, and some have simply reimagined the geometry of Chess while still playing on a flat 8x8 board. One of the games people have tried to play on a spherical board is Cylindrical Chess, in which each rank loops back into itself, as it would on a sphere, cylinder, or circle. In personal correspondence, Mark Davis has told me that his Spherical Chess follows the same rules as his Round Chess, and the rules he described were those of Cylindrical Chess. Likewise, János Boholy's first version of Globe Chess is also Cylindrical Chess. However, this page will not be about just any adaptation of Chess that can be played on a spherical board. Rather, it will be about those that conceive of the board as a sphere and make use of spherical qualities that cylinders and circles do not have. The main thing that distinguishes a sphere from a cylindar or a circle is that movement may loop around it in any direction, not just in horizontal or east-west directions, as they do in Cylindrical Chess. In the games described on this page, movement may also loop in vertical or north-south directions. This page is on attempts to describe how Chess could be played on a regular 8x8 Chess board turned into a sphere. It will not be concerned with Chess variants played on other spherical boards or with other games besides Chess that could be played on a spherical board.
Since the important thing about Spherical Chess is that the board is conceived of as a sphere, it may be played on a standard 8x8 Chess board. As in Cylindrical Chess, which is usually not played on a cylindrical board, the ranks loop back into themselves. So, horizontal movement of a Rook along a rank will take it from the left side to the right side or vice versa. You may think that direction shouldn't matter on a sphere, and the files should also loop back into themselves too. While that will work for boards of some dimensions, it does not work for an 8x8 board. To fit an 8x8 board onto a sphere in this manner, each rank and file would have to loop around the sphere, such that it has four spaces on one side and four on the other. But this would limit each side to 4x4 and the whole board to 32 spaces. While a 4x16 board could be placed on a sphere in this manner, an 8x8 board whose ranks and files each loop back into themselves is best visualized as a torus, which is a cylinder whose ends have been brought together into a loop.
Instead of treating the board as doughnut-shaped, these games treat ranks and files as though they were lines of longitude and latitude. Ranks are like lines of longitude encircling the globe. Files are like lines of latitude extending from one pole to the other. While the ranks lie parallel to each other, the files meet at the poles. Instead of a file looping back into itself, it loops into the file that lies four files away. This may not seem intuitive on a regular chess board, but if you play on an actual sphere or on a 2D representation of the two hemispheres, as shown in the diagrams below, this becomes much clearer. Each end rank is wrapped around the pole such that when a Rook passes over the pole, it naturally goes to a space in the same rank that is four spaces away.
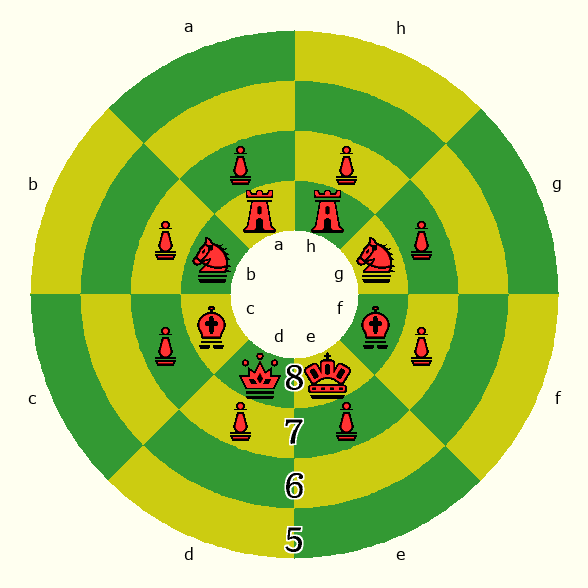
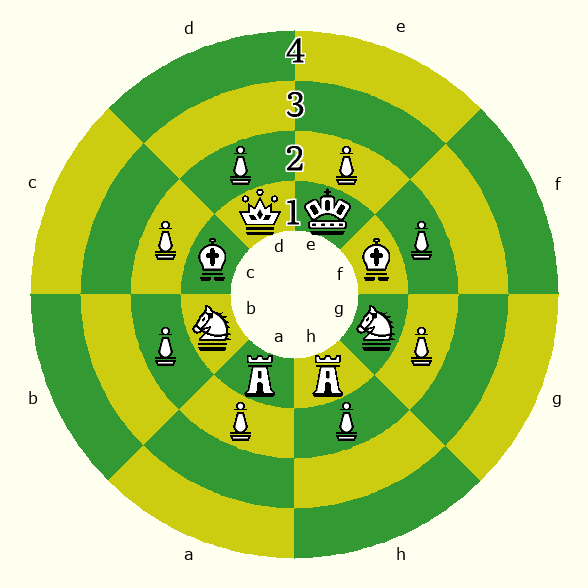
Each diagram shows one hemisphere. Black is at the north hemisphere, and White is at the south hemisphere. Instead of placing the files in the same locations on each hemisphere, the files are aligned in a manner that makes the two images look more like the usual Chess board when the south hemisphere is placed below the north. This also fits with how each hemisphere would be viewed from outside the sphere. If you played the game on a globe with magnetic pieces, each image shows how one hemisphere would look if you rotated it to the top. Each image is also based on the idea of curving a group of four ranks in the manner that naturally places the first or last rank closest to the center.
While the trans-polar movement of the Rook is intuitively obvious on such a board, the trans-polar movement of the Bishop is not. This has led to different ideas on how the Bishop should move, and this has had implications for how the King, Queen and Knight should move. This page will provide a historical retrospective on adaptations of Chess to a spherical board, beginning in the 1950s and continuing into the 21st century. The main difference between these versions is how they handle Bishop and Knight moves. A Queen will move as a Rook or a Bishop, a King will move as a Queen one space, and a Pawn, having no opportunity to make a trans-polar move until it has already promoted, will move as it does in Cylindrical Chess.
H. D. Grayber's Version (1950s)
In The Encyclopedia of Chess Variants, Pritchard says that the first spherical Chess variant may be one that H. D. Grayber invented in the 1950s. This game is mentioned by Joseph Boyer without description, but Pritchard presumes it may be the same game described by Pierre Berloquin in Cent Jeux de Table.
Bishop moves
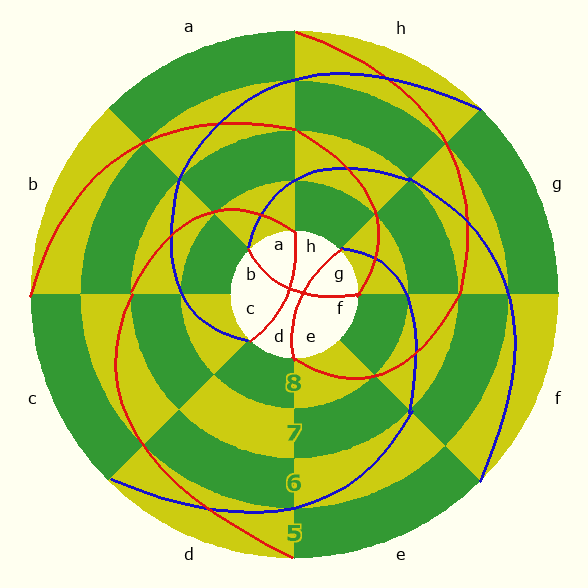
As in Chess, the Bishop normally moves in a diagonal line, passing through the corners of spaces while remaining on the same color. In The Encyclopedia of Chess Variants, Pritchard gives an example of how the Bishop allegedly moves in H. D. Grayber's version. He says "The trans-polar move of a B forms a loop, its path re-crossing the 2nd/7th rank square (Bh3-a2-b1-h1-a2-b3)." From this example, we may gather that when a Bishop makes a trans-polar move, it reverses longitudinal direction to the nearest diagonal of the same color, then continues in the same longitudinal direction it was going before but now in the opposite latitudinal direction. While this example is cut short, Anthony Dickins, writing on Miller's version, which Pritchard says has the same Bishop move, extends it to an entire circuit around the board. In A Guide to Fairy Chess, he writes
the Bishop has a most peculiar move, in which it covers all 32 squares of one colour twice before it returns to the original square – so a Bishop on g4 may move h3, a2, b1, and then on through the Polar Point in the same type of spiral, in this case a counter-clockwise spiral, to h1 and then to a2, b3, etc. to g8 then to e8 and on to f7, g6, etc. to d1, then b1 and on to c2, d3, to a8 then to g8 and on to h7, a6, b5 to f1 then to d1 and on to e2, f3, g4 (the original square, but with a different direction of travel, for we are only half way round) h5, a6, b7 to c8 then to a8 and on to b7, c6 etc. to h1 then to f1 and on to g2, h3, a4, b5 to e8 then to c8 and on to d7, e6, f5 and finally back to g4!! There are four such tours that the Bishop can make from g4. (19)
Here are some diagrams showing an extended version of Pritchard's example, which does overlap a lot with that of Dickins. You can see that it is quite complex and torturous, making the Bishop a very powerful piece. To make intersecting lines easier to follow, movement south is colored red, and movement north is colored blue. Contrary to what Dickins has said, it looks like the Bishop does not actually cover every space of the same color twice before returning to its origin. In this example, it misses one space of the same color, and it passes through some only once, though it does indeed pass through many spaces twice before returning to its origin. Even in his own example, which does seem to cover every space of the same color twice when I played it out, he returns to that space before its move has covered every other space of the same color twice, and he stops only when he comes back to it a second time. In practical play, there should never be any need to calculate the ability of a Bishop to move past its own space, because it could simply move in the other direction to begin with.
Knight moves
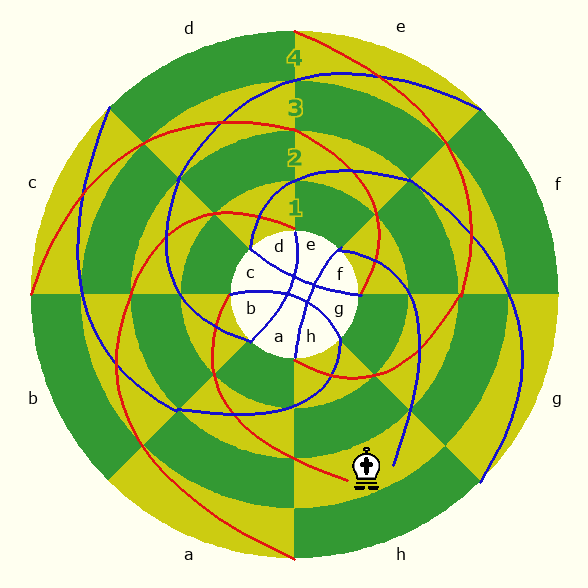
In this game, Knights that are one or two ranks away from the pole have only six possible moves instead of eight. The example Pritchard gives is "Ng2: a1,a3,h4,f4,e3,e1 Ng1: a2,b2,h3,f3,e2,d2." This is illustrated below. The white dots show where the g1 Knight can go, and the red dots show where the g2 Knight can go. Notice that the g1 Knight has two moves to spaces of the same color. These are its transpolar moves. They go two spaces past the pole and turn left or right one space. The Knight on the next rank up has only regular Knight moves, but only six are available this close to the pole. Further away from the pole, each Knight has eight possible moves, as it maximally does in Chess.
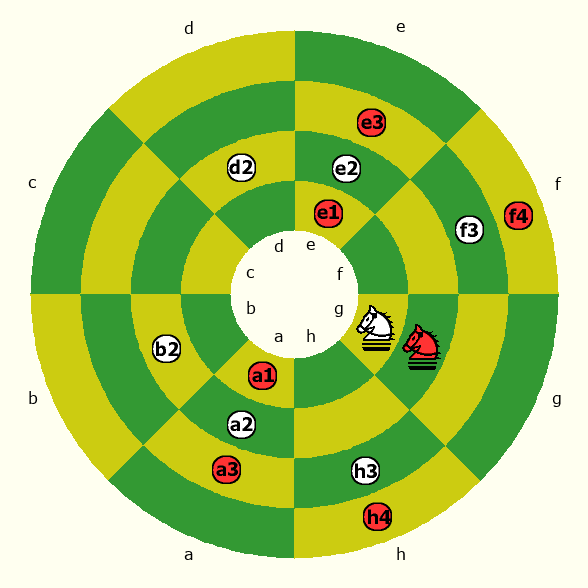
Don Miller's Version (1965)
In Miller's version from 1965, Bishops move the same as they do in the version attributed to Grayber, but a Knight that is two ranks away from a pole now has eight possible moves instead of just six.
Knight moves
The diagram below illustrates two examples Pritchard gives for how the Knight moves in Miller's version. In one example, a Knight on g1 can move to a2, b2, h3, f3, e2 or d2. In another example, a Knight can move from g2 to a1, a3, h4, f4, e3, e1, b1 or d1. The white circles mark the space the White Knight could leap to, and the red ones mark the spaces that Black's Knight could leap to. For the Knight next to the pole at g1, only six moves are available. For the Knight at g2, eight moves are available. In each example, there are two spaces the Knight could reach of the same color. These are the spaces it may reach through transpolar movement.
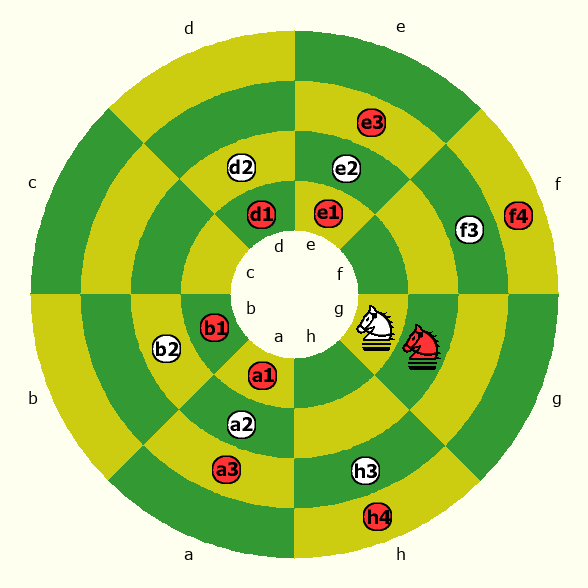
When the Knight is next to the pole, it can leap to the spaces that could be reached by going through the pole to the space on the other side, then moving one more space diagonally outward. This can be seen where the Knight at g1 can leap to b2 or d2. When the Knight is on the 2nd or 7th rank, it can leap to the space that could be reached by moving one space vertically toward the pole, then one space diagonally outward in the manner described for the Bishop when making a trans-polar move. These spaces may also be reached by moving one space diagonally toward the pole, then moving vertically across the pole to the space on the other side. This can be seen where the Knight at g2 can move to b1 or d1.
Peter Yapsan's Version (1971)
Peter Yapsan's Spherical Chess is described in an article I purchased off of ebay called "Infinite and Spherical Chess, or Playing Chess on a Simulated Sphere." He initially treats these as the same game. Speaking of the former, he says "Instead of making Chess more complicated, Infinite Chess completes the natural development of chess. Not a chess variant, Infinite Chess strictly, completely and accurately follows every rule of chess." A little later on, he says "When played on a circular board, Infinite chess is called 'Spherical Chess'." Here is a photograph of the sort of board he has in mind. This board uses different colors and markings to aid the visualization of moves. Unfortunately, this is the only image provided of the board, and there is no image of the board by itself or in color. The setup in the photo has transposed the Knights and Bishops from the usual setup, but since Infinite Chess does not change the setup of Chess, and nothing in the text corroborates that Spherical Chess has a different starting position, I assume a mistake was made before the photo was taken.

Bishop moves
Pritchard has incorrectly reported that "A diagonally-moving piece (K, Q, B) makes an inter-polar move (e.g. a7-b1) but not a trans-polar move." But Yapsan says nothing about inter-polar moves. Under the "TRANS-POLAR MOVE" section, he writes, "A radially or spirally moving piece which lands or has landed on a [sic] inner or outer circumference space may move across the pole to the opposite space on the same circumference by making a radial move." At this point, it's important to note that by radial, he means vertical. On his circular board, one pole is at the center, and one is on the edge, and by "inner or outer circumference" he means the end ranks closest to each pole. Whether a piece is moving vertically or spirally (diagonally), it makes a trans-polar move by moving vertically to the space that would be directly opposite it when the rank is encircling a pole. This is the space that is four spaces away in the same rank. Under the "SPIRAL (DIAGONAL) MOVE" section, he writes "When approaching either pole in a clockwise or counter-clockwise direction, exit the pole in the opposite spiral direction." From this, we may understand that a diagonal move crosses the pole vertically to a space of the same color, which is four spaces away in the same rank, then continues in the opposite direction it was going in. If it was going north west, it would go south east after crossing the pole. Such a move is color-bound, and the full circuit that a diagonal move may take is 16 spaces. Underneath the section "NUMBER OF SPACES IN ONE DIRECTION A PIECE MAY OCCUPY AND COMMAND," Yapsan gives a value of 16 for the Bishop. This gives confirmation that the Bishop in this game does not have a complicated move like it does in Grayber's or Miller's.
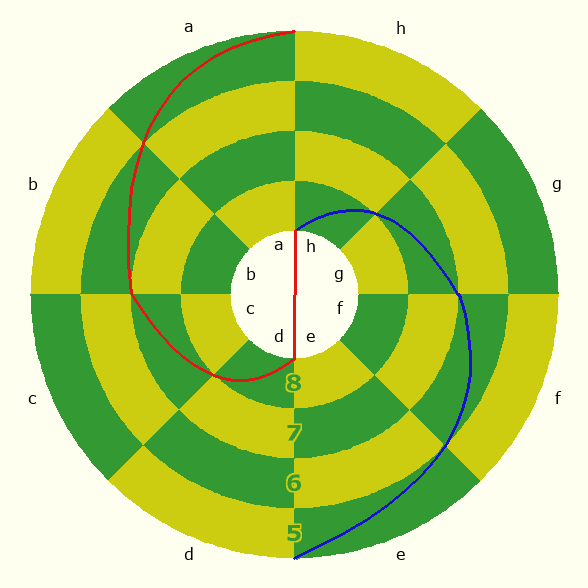
The following diagrams show an example of a complete Bishop loop. I have used red for moving south and blue for moving north. So, the Bishop starts at g3, goes south to f2 and e1, crosses the pole to a1, continues north to b2, c3, and d4, crosses the equator to e5, continues north to f6, g7, and h8, crosses the pole to d8, continues south to c7, b6, and a5, crosses the equator to h4, and ends up at g3, where it started. To avoid making the diagram too complex, this shows only one path the Bishop could move along. Like the regular Bishop, it can go in any diagonal direction.
Knight moves
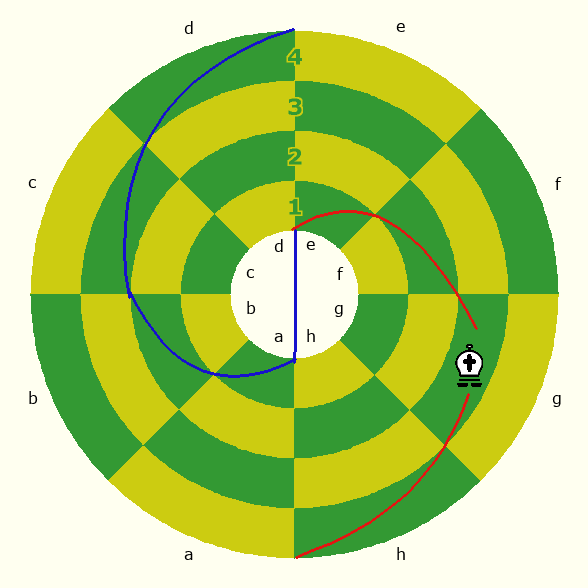
Yapsan does not provide a diagram of where the Knight can leap, but he does give a written description. He says "The trans-polar move is guided by moving straight across to the space of the same color. After the trans-polar move the move may be continued. The knight moves radially across the pole when making a radial move; its move is then completed by a circumpolar move." By circumpolar, he means a circular move around a pole, which would be a horizontal move on a regular Chess board. Additionally, he says "The knight moves one space in a circumpolar (radial) direction and two spaces in a radial (circumpolar) direction, or vice versa, always in the same general direction. The knight can move even when the intervening spaces are occupied." Since cicumpolar moves are horizontal, and radial moves are vertical, the parenthesized words do not mean the same as the words following them but are instead alternatives. That means that a Knight may leap to any space that may be reached by any combination of two consecutive moves in one circumpolar direction and another move in a radial direction or two consecutive moves in a radial direction and one more in a circumpolar direction. With this in mind, the following movement diagram should depict how Knights near a pole may move:
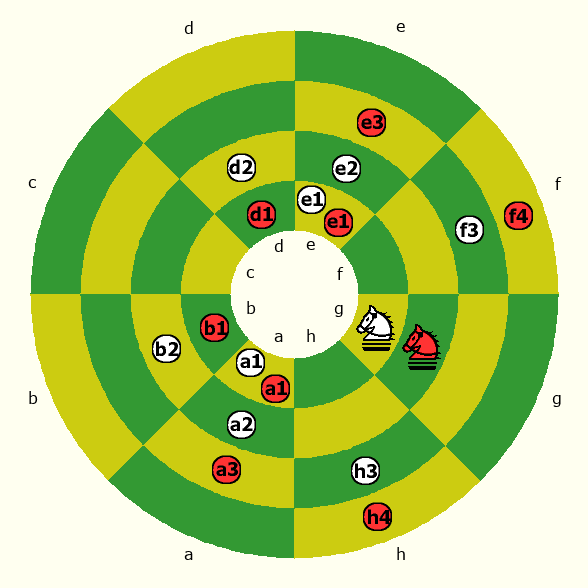
In this diagram, red dots show where Black's Knight can go, and white dots show where White's Knight can go. Unlike in Grayber or Miller, each Knight can reach 8 spaces from any position. While Yapsan does not go into the detail shown in the diagram, he does give a value of 8 for the Knight in the section "NUMBER OF SPACES IN ALL DIRECTIONS A PIECE MAY OCCUPY AND COMMAND SPACES AFFECTING MOBILITY." While he does give multiple values for Queen and Pawn, presumably due to having a different number of possible moves from different positions, he gives only the single value of 8 for the Knight. This may be taken as confirmation that he does not limit the moves of Knights close to a pole, as Grayber and Miller do.
Castling
When castling, a King may move toward a Rook from either side. In an example from Infinite Chess, which also applies to Spherical Chess, White has a King on e1 and a Rook on h1, but castles by moving to c1 and the Rook from h1 moving to d1. Infinite Chess also allows vertical castling when the King and Rook are four spaces away (such as a1 and e1), but this option is not included in Spherical Chess.
Stationary (Infinite) Moves
When a Bishop, Rook, or Queen can make a move completely around the board that is able to return to its original space, Yapsan counts such a move as legal.
Leo Nadvorney's Version (1975)
Nadvorney's version was a deliberate revision of Miller's version, and it may have been made without knowledge of Yapsan's version.
Bishop moves
Unlike the Bishop in Miller's version, the Bishop in this version changes color when it makes a trans-polar move. When it reaches the pole, it goes directly from the corner its movement would normally continue through if there were another rank to the corner directly opposite, then continues its movement through the opposite corner of the space with a different color from the one it just came from. This can also be described as moving three spaces back along the rank, changing latitudinal direction, and continuing in the same longitudinal direction. So, the main difference from Miller's version is how far along the rank the Bishop moves when crossing the pole. For Miller, that move is two files back, and for Nadvorney, that move is three files back. Note that it is three files back, not three files forward. It is illegal, for example, to move a Bishop from h3 along the path g2-f1-c1.
Pritchard gives the example of moving a Bishop from h3 along the path of a2-b1-g1-h2-a3. An earlier version of this page uses the example of moving a Bishop from h3 along the path g2-f1-a1-h2-g3 and the example of a Bishop moving from d3 along a path of e2-f1-c1-d2-e3. But none of these examples show the complete circuit the piece can make. In the following two diagrams, a Bishop makes a complete circuit from g3 to g3. To make the diagrams clearer, I used red for movement south and blue for movement north. Starting from g3, the Bishop goes south to f2 and e1, crosses the pole to h1, continues north to g2, f3, and e4, crosses the equator to d5, continues north to c6, b7, and a8, crosses the pole to d8, continues south to c7, b6, and a5, crosses the equator to h4, then ends up at g3, where it started.
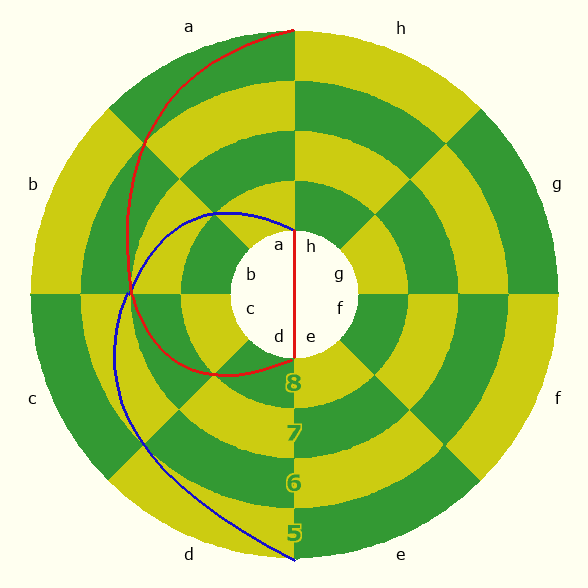
Knight moves
Pritchard mentions that the Knight always has eight spaces it can move to. He does not give any examples, but the move can be understood as a leap to a space that may be reached by one orthogonal move, followed by one diagonally outward move. These are the same spaces a Knight may reach in Yapsan's version, and the diagram can be found above.
These moves can be confirmed by examining the following diagram, which has only cosmetic differences from one provided by Nadvorney. This diagram shows the regular Chess board in the middle, and around the edges, it shows the spaces that may be reached by orthogonal, diagonal, and Knight moves that move away from the edges for up to two spaces away.
| c7 | d7 | e7 | f7 | g7 | h7 | a7 | b7 | c7 | d7 | e7 | f7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| c8 | d8 | e8 | f8 | g8 | h8 | a8 | b8 | c8 | d8 | e8 | f8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| g8 | h8 |
|
a8 | b8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| g7 | h7 | a7 | b7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| g6 | h6 | a6 | b6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| g5 | h5 | a5 | b5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| g4 | h4 | a4 | b4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| g3 | h3 | a3 | b3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| g2 | h2 | a2 | b2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| g1 | h1 | a1 | b1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| c1 | d1 | e1 | f1 | g1 | h1 | a1 | b1 | c1 | d1 | e1 | f1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| c2 | d2 | e2 | f2 | g2 | h2 | a2 | b2 | c2 | d2 | e2 | f2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The only difference from Miller's version is that the Knight at g1 can also move to a1 or e1. These are the spaces that may be reached by first moving one space longitudinally, then moving diagonally through the pole. Since the diagonal move through the pole takes it back three spaces along the rank, it is able to leap to spaces two files away on the same rank when it is next to the pole.
Castling
Pritchard says this version has the same castling rule as Peter Yaspan's version. As already mentioned, this means that a King may castle with a Rook by approaching it from either side. So, in addition to regular castling, a King may castle with the h Rook by moving to the c file or with the a Rook by moving to the f file. This is allowed, of course, only when all other castling conditions apply.
No Stationary or Infinite Moves
Unlike Yapsan's version, Nadvorney's does not allow moves that do not change the position of a piece.
Rules of Nadvorney's Version
- The board is spherical, as described above:
- A Rook moving through a pole emerges on the opposite side and continues in a straight line, as for example Ra3-a1-e1-e4.
- A Bishop moving through the pole from a given square emerges one square away from the diametrically opposite one, depending on which direction it is moving. Examples are Bh3-g2-f1-a1-h2-g3 and Bd3-e2-f1-c1-d2-e3, but not Bh3-g2-f1-c1.
- Moves of other pieces can be inferred from the above; for example, a knight move can be regarded as a 1-step R move followed by a 1-step B move, such as Sd1-h1-g2/a2.
- Since are no edges, pieces can move around the board along the ranks
as in Cylindrical Chess.
This requires two ruling like those for Cylindrical Chess: - A piece may not make a move around the board (like Rh3-a3-h3) that leaves the position unchanged, nor may it make an infinite (never ending) move.
- Two new forms of castling are possible, if the usual condition are fulfilled: Ka1-c1, Rh1-d1 over a1 (written C0-0-0) and Ke1-g1, Ra1-f1 over h1 (written C0-0).
The Laws of Chess apply, except as follows:
Notation
On transpolar moves it may make things clearer to indicate the square from which the pole was crossed, but this is not necessary.
János Boholy's Globe Chess (1987)
On the website Globe Chess, János Boholy describes four Chess variants that can be played on a sphere. Although records of his website on archive.org date back to 2006, he patented the game with the Czech Republic in 1987 and with Slovakia in 1993. (See BOHOLY, János: Globe chess.) Of the four versions he describes, only the second, which he calls The optimal version of Globe – chess, is a true spherical adaptation of Chess. The first, as previously mentioned, is Cylindrical Chess. The third, which treats the poles as spaces, is similar, if not identical, to Martin Nelson's 1976 version of Spherical Chess, the fifth and last game Pritchard covers in his "SPHERICAL C" article for his *Encyclopedia*. The other four are the four previous ones listed on this page. This one is not a strict adaptation of Chess to a spherical board, because it adds two new spaces that radically transform the game. The fourth is just a setup change that may be applied to any of the earlier versions.
Although his optimal version is played on 64 spaces, it does introduce the idea that the poles are neutral spaces. Pieces may not land on them, but they do play some role in affecting how pieces move.
Knight moves
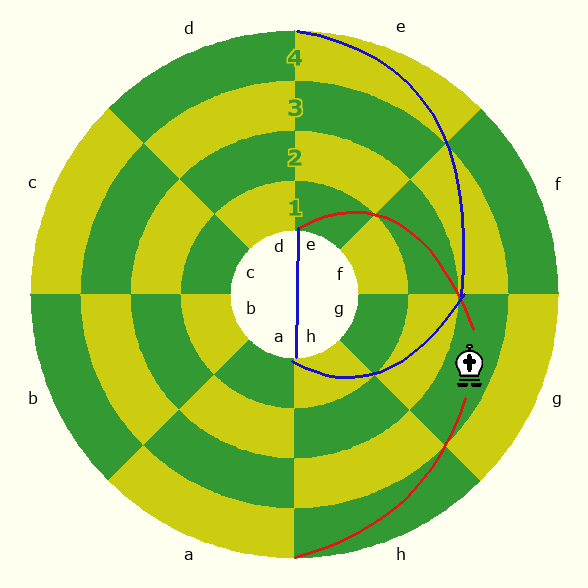
In describing how the Knight moves, he says a Knight on b1 can move to a3, c3, h2, d2, g1, and e1. For consistency with other diagrams, I shall shift this to g1, from which a Knight may move to h3, a2, b1, d1, e2, and f3. These six spaces are different than those the Knight can move to in Grayber and Miller, because Boholy is counting the pole as one of the spaces the Knight leaps over. Instead of its L-shaped leap from g1 going through c1 and c2, and then to b2 or d2, it goes through the south pole and c1, then turns to either b1 or d1. Applying the same principle to a Knight on the second rank, a Knight on g2 could move to h4, a3, a1, e1, e3, or f4. This is also six spaces, since two different pairs of routes end up on a1 or e1. It may reach a1 by going left two spaces and south one, or by going south two spaces, which takes it to the pole, then turning left. Likewise, e1 may be reached by right-right-south or by south-south-right.
Bishop moves
The Bishop moves in an S curve when passing through a pole. It crosses a pole by moving directly across, just as a Rook does, and then it turns in the opposite direction it was moving in when heading toward the pole. For example, if it was going south west while heading toward the south pole, it will turn north east after crossing it. Its move is the same as it is in Yapsan's version.
King moves
Because the diagonal move of the Bishop is no different than that of the Rook, the King can cross a pole only by moving directly across it. This gives the King six possible moves when at the pole. Because the poles are treated as neutral spaces, a King may pass over a pole only if it is not attacked by an enemy piece. This is straightforward for Rooks, Bishops, and Queens. Since they move space-by-space, the pole may be considered attacked by one of these pieces if its path of legal moves would take it up to or across the pole. Still on the principle that the pole is a space on the board, the pole would be attacked by a Knight if it has a leap that would take it directly to the pole. A Knight on the first rank could go left or right twice, then go vertically into the pole. And a Knight on the second rank could go left or right once, then two spaces vertically toward the pole. Knights further away are too far away. So, any enemy Knight on the first or second rank from the pole, though no further than that, can be considered to attack it.
The castling rule seems to be no different than that in Chess. Boholy says "On the annular first rank the king can castle either side, with either of the rooks. (On the left or right side with a rook that hasn’t moved yet)." While this is ambiguous enough to possibly include castling with a Rook from its other side, he may just be referring to either side of the King, which would be fully consistent with how castling works in Chess. More tellingly, he does not raise the possibility that a King could castle with a Rook from the other side of the Rook. The only new option he mentions for castling is that a kind of castling position is achieved automatically as soon as a rank is cleared of every piece except the King and the two Rooks. In this position, both Rooks are already protecting the King from each side.
Stationary or Infinite moves?
Boholy does not raise the possibility of such moves. In describing the Rook move, he gives examples and lists each space the Rook may move to, none of which include the space the Rook began on. But in describing the Bishop move, the list of spaces he gives does end with the space the Bishop began on. This may just be to illustrate how a Bishop's path loops back to its original position. Since the examples for the Rook did not include the option of returning to its own space, it's presumed that the Bishop and Queen cannot, and that this game does not allow stationary or infinite moves.
Tony and David Welman's Global Chess™ (1989-1997)
In 1997, Global Chess International, Inc., which was formed in 1996, released the game Global Chess. But even earlier in 1989, the inventors of this game, Antonie and David Welman of South Africa, applied for United States patent US5145181A, European patent EP0371623A1 and Australian patent AU629587B2 for the mechanism that would be used to play this game. So, they may have already invented the game by 1989 or earlier. As can be seen in the photograph of the Global Chess set below, this represents a sphere with two flat hemispheres. Each hemisphere is a gear, and when you turn one, the other rotates in the opposite direction so that the same file will line up where they touch. This is to help with the visualization of moves. Each space is also marked with its coordinate, though these can be hard to read in the photo.

This game is very similar to Yapsan's version, the main differences being that castling works as it does in Chess, and no mention is made of stationary moves being legal. The diagram for the Knight does show that a Knight on the rank next to a pole can reach up to eight spaces, but it does not specifically cover the moves available to a Knight on the second rank from a pole. It presumably has eight moves too, as in Yapsan's or Nadvorney's version. Since the website for this game is down, copies on archive.org are missing some graphics, and it is presumably out of business, here is an image made from a couple scans of the rules card that comes with the game. This is provided as documentary evidence of its rules. You may open it in a new tab to see it full size.

Contrary to the Knight diagram on the card labeled E, an archived copy of the Knight page does not include the ability of a Knight in the rank next to a pole to move to a space two files away in the same rank. It may be that the creators of the game later reverted to a rule in line with Miller's version. This would also make the game more like Boholy's Globe Chess.
Stationary or Infinite moves?
The rules do not mention the possibility of such rules. Furthermore, the diagrams I and N, which show complete diagonal loops for the Bishop and Queen, do not show movement continuing to the space the piece started from. So, I would presume that stationary or infinite moves are not allowed.
Antonie Welman's Sphere Chess (2009)
I came across Sphere Chess after I learned that Tony Welman, a.k.a. Antonie Welman, was the creator of a game called Sphere Chess at the now defunct URL spherechess.com. Archives of the site go back to 2011, and it has a copyright date of 2009, which is when I presume Welman created this successor to Global Chess. Although this website is no longer up, I did find a link to the rules on a forum that is still up: How to Play Sphere Chess. It is very similar to Welman's earlier Global Chess, but it has some differences. Knights do not make trans-polar moves in Sphere Chess. Instead, they just move around the pole. The diagram for the Knight shows the Knight on b1 able to reach d2, c3, a3, and h2. By extrapolation of the rule, a Knight on b2 should be able to reach d1, d3, c4, a4, h3, and h1. With only four and six possible moves on the ranks nearest to the pole, it is the weakest Knight in any version. This also fits in with the online rules for Global Chess having a less powerful Knight than the rules included with Global Chess sets in 1997. The King is now as immobile as the Chess King. It cannot cross the pole or the a/h divide. This fits in with Global Chess not providing the option of castling with a Rook by moving toward it from either side. Although its castling rule, as described, sounds consistent with allowing castling from either side of a Rook, it does not raise this as a possibility, and this would not fit in with the spirit of not allowing the King to cross the a/h divide.
Joshua Chao's Globe Chess / Dot / Chess on the Dot (2008-2014)
In 2008, Joshua Chao of Taiwan got the idea to adapt Chess to a sphere, and he made a prototype spherical board he dubbed Globe Chess. He then made a digital game called Dot for iOS for which he won the Red Dot Award in 2010. Four years later, he set out to make a wooden version of Dot, which he called Chess on the Dot. While Dot for iOS no longer seems to be available, and the images of its screen shots are mostly illegible, it would appear that Dot and Chess on the Dot are the same game. One screenshot for Dot says its rules are the same as Chess, and his link to his "Dot" booklet is the same as his link to his "Chess" booklet. For our purposes here, we'll use the name Chess on the Dot, which is more clearly the name of a Chess variant than Dot, and which has not already been used by another inventor.
Having already described some very similar versions, Chao's game can be described very briefly. It is nearly identical to Yapsan's version and the Welmans' Global Chess, which both preceded it. It is the same as Yapsan's version except that it forbids stationary moves. His "Chess" booklet includes the rule "A piece cannot move into a square which is the very same square it comes from by walking a loop, because such movement leads to no change." It is the same as the original version of Welman and Welman's Global Chess except that it allows castling from either side. His "Chess" booklet shows a diagram in which a King on e1 may castle with the Rook on h1 by moving to c1. Technically, Chess on the Dot also has only one difference from Nadvorney's, though it's the more far-reaching difference of how diagonal moves work. While the black and white diagrams in his "Chess" booklet do not make it clear, his Essay on Chess on the Dot includes animations explicitly showing how a Bishop moves in a single direction. In other respects, it is just like Nadvorney's version.
Summation
Analysis
As we have seen, people have repeatedly tried to adapt Chess to a spherical board. Thanks to information about past Spherical Chess versions not being centralized and readily available, the creators of these games often worked without knowledge of past versions. In Nadvorney's case, we do know that his game was a revision of Miller's version. However, Yapsan saw his game in the line of 3D adaptations of Chess, and although he mentions Cubic Chess and Space Chess, he does not mention any prior version of Spherical Chess. Boholy mentions that he first conceived of Globe Chess at the age of 13, which would be around 1950 if he was 50 when he got his patent in 1987. The creators of some of these games also take pride in coming up with their version of spherical chess. Yapsan described Infinite Chess, and by extention Spherical Chess, as "the most practical, natural, realistic and legitimate three-dimensional chess possible." Boholy and the Welmans got patents, and Chao displays an award he won for Dot. Although each of these attempts is different from the others, certain design decisions have each been made by a majority of the game designers. Let's list the most popular design decisions from among these seven attempts and see what we get.
For the diagonal move, the most popular is the simple colorbound version that goes directly through the pole in a vertical direction and then completely reverses direction from whatever direction it was going in before. This affects Bishops, Queens, and Kings. With this type of diagonal move, a King by a pole has only six possible moves. This is common to Yapsan, Bolholy, Welman, and Chao, which is 4 out of 7. If we count Nelson's version, which treats the poles as spaces, then 5 out of 8 support this type of diagonal move. While I won't count Sphere Chess separately from Global Chess here, it is worth noting that Welman did not change this feature of the game.
For the Knight move, the most popular is for the Knight to have eight possible moves from any space on the board. This is common to Yapsan, Nadvorney, Welman, and Chao, which is 4 out of 7. However, given that Welman later changes this, we might count this as 3 out of 7. Nevetheless, the other options remain divided. Grayber, Miller, and Boholy each give different rules for how the Knight moves, and even if Welman coincides with one of them, that's still only 2 out of 7.
For castling, the most popular option seems to be to castle as in Chess without any extra option of castling with a Rook on its other side. This is presumably common to Grayber, Miller, Welman, and Boholy, which is 4 out of 7. Yapsan, Nadvorney, and Chao all add the extra option of allowing a King to castle with a Rook by moving toward it in what would usually be considered the wrong way. I think this option is more fitting with the idea of spherical chess, and those who didn't include it might not have thought about it. It's also possible that it was included in Grayber's or Miller's version, but the secondary sources we know of these games from have failed to mention it.
On the matter of the King crossing the pole, most put no restriction on this ability. For Grayber, Miller, Yapsan, Nadvorney, Global Chess, and Chao, the pole is just an intersection between spaces, and the King may move across the pole as freely as it may move across a diagonal that is controlled by the opponent. But for Boholy, the pole is a space that pieces may cross but not land on, and the King may cross it only if moving to the pole would not place it in check. In Welman's Sphere Chess, the King may not cross the pole at all.
On the matter of the King crossing the a/h divide, most allow this, and only Welman's Sphere Chess does not.
On the question of stationary moves, only Yapsan explicitly allows them, and only Nadvorney and Chao explicitly forbid them. This question doesn't come up in the description of most variants, and this may be because a stationary move is a contradictory idea. A move normally involves a change in position, and a stationary move does not. On this basis, I would expect that stationary moves are not allowed in any game unless it explicitly allows them. So, it looks like the majority do not allow stationary moves.
On other matters, there is univeral agreement. Rooks and Pawns move the same in all versions, and rules concerning how the game is won, lost, or drawn are all the same.
Of all the versions described, the original version of Global Chess is the one that represents what appear to be the most popular design decisions. However, Global Chess later reduced the movement capability of the Knights, and in Sphere Chess, also made by one of the Global Chess inventors, the movement capability of the Knights got reduced even further, and the King became restricted to moving as though it was on a square board. These changes show that the inventors of Global Chess, or at least Tony Welman, being the principle one involved, was dissatisfied with the original design of Global Chess and through playtesting came to prefer some different rules.
Whether or not these decisions made the game better, I think they moved the game away from being a true spherical analog of Chess. Judging the games strictly on how well they accomplished this goal, I think that Chess on the Dot is the most straightforward adaptation of Chess to a spherical board. Unlike Nadvorney's, the Bishops are color-bound, and unlike Miller's, the Bishops do not have a complex zig-zagging move that can potentially cover every space of the same color. Unlike Yapsan's, Chess on the Dot forbids stationary moves. Unlike Global Chess, it doesn't impose artificial barriers on castling that are simply an artifact of the square shape of a Chess board.
Rules and Notation sections of Navordney's version mainly written by Alessandro Castelli; new material and diagrams by Fergus Duniho.
WWW page created: September 30, 1996. Last modified: July 29, 2021.
