Comments/Ratings for a Single Item
An extension in your sense is not the subject of discussion.
You can certainly scrap the entire concept. Agreed, but which concepts in the CVP stand up to your inspection?
Mind games should be able to be discussed. Or do you have a different opinion?
Here are the rules of Chess66 as I've written them up for Game Courier. Apart from a change to the naming convention for the new spaces, is this complete and fully accurate? Note how I've divided this into five sections. These are the geometry of the board, the difference that Switches make, how spaces in a Switch count as separate spaces, how spaces in a Switch are sometimes treated as the same space, and how the individual pieces move.
Rules of Chess66
Chess66 is an adaptation of Chess to a board with a different geometry. Where no difference from Chess is noted, it follows the rules of Chess.
- Its board has two extra spaces that each overlap with a neighboring space and push the rank it is on over by half a space. A4 overlaps with a4, pushing the 4th rank half a space right. H5 overlaps with h5, pushing the 5th rank half a space left.
- Because its ranks and files no longer line up neatly on a Cartesian grid, movement is based only on geometrical relations and not on the coordinate system.
- Lateral movement is allowed through the sides of spaces, and lateral movement in the same direction goes through the opposites sides of spaces. Because of this, vertical movement may sometimes shift the file named by the coordinate system.
- Diagonal movement is allowed through the corners of spaces that do not share any sides, and diagonal movement in the same direction goes through the corners at opposite ends of spaces.
A Switch is a pair of overlapping spaces that come together at one end and branch off at the other. In doing so, they allow some new movement options:
- At its narrow end, each space in a Switch shares the same side with an adjacent space. This allows a Rook or Queen to move through the narrow end to one of two different files. In this way, a Rook or Queen can checkmate a King without assistance from another piece.
- From the broad end, a Rook or Queen can move through the Switch to the same file, providing a new way for double attacks to work.
- Also at the narrow end, each space in a Switch shares a corner with another adjacent space that neither one shares any sides with. Through this corner, diagonal movement is able to change color. So, a Bishop that moves to A4 or to H5 may move away on a subsequent turn on a different color. This allows Bishops to switch color, giving a Bishop the power to reach every space on the board.
Although the two spaces in a Switch overlap, they count as separate spaces.
- A piece moving to a Switch must move to one space or the other. For example, a Pawn on a2 can make a double move to either A4 or a4.
- While some paths can lead to either Switch, others lead to only one space or the other in a Switch. For example, a Bishop on e8 can go to A4 or h5, and a Bishop on d1 can go to a4 or H5.
- The movement options available to a piece on a Switch depend upon which space of the Switch it is on. For example, a Pawn on A4 can proceed only to a5, and a Pawn on a5 can proceed only to b5. Also, a Bishop on A4 can move away on either light or dark spaces, but one on a4 can move away only on light spaces.
Because the two spaces in a Switch overlap, they are treated as the same space in some respects:
- The two spaces in a Switch cannot be occupied simultaenously.
- It is illegal to pass through a space in a Switch if the other space is occupied.
- A piece may move to a space in a Switch only if both spaces in it are empty or one is occupied by an enemy piece. If a piece moves to the empty space in a Switch, and the other space is occupied by an enemy piece, that piece is considered captured.
- It is not legal to move from one space in a Switch to the other. Instead, A4 is treated as though it were horizontally adjacent to b4, and H5 is treated as though it were horizontally adjacent to g5. This affects the movement options for Rooks, Queens, Kings, and Knights

The King leaps one space in any lateral or diagonal direction. It may castle with a Rook on its first move so long as it is not in check, there is nothing in between it and the Rook, it doesn't pass through check while castling, and the Rook hasn't moved. In castling, it moves two spaces toward the Rook, and the Rook moves to the space the King passed over.

The Queen may move as a Rook or a Bishop.

The Rook may move any number of spaces in any lateral direction until it reaches an occupied space or Switch.

The Knight can leap directly to any space that could be reached in two one-space moves except for those reachable by two in the same direction. Since a piece on A4 or H5 can move directly to b4 or g5, a Knight on one of these can leap further away than a Knight can normally leap.

A Bishop may move any number of spaces in any diagonal direction until it reaches an occupied space or Switch.

The Pawn may move one space straight forward without capturing, or it may move one space diagonally forward to capture. On its first move, it may move two spaces forward without capturing so long as it isn't blocked. If this move takes it over a space an enemy Pawn could have captured it on, that Pawn may immediately capture it by en passant, moving to the space it passed over. On reaching the last rank, it must promote to another piece. This may be any piece except a King or another Pawn.
 H. G. Muller wrote on Sun, Nov 13, 2022 08:24 AM UTC:
H. G. Muller wrote on Sun, Nov 13, 2022 08:24 AM UTC:The definition of the Knight move is not correct. On an undistorted board it would allow the Knight to also move like Wazir or Ferz. This could be fixed by also excluding moves that are reachable in a single step.
Diagonal movement is allowed through the corners of spaces that do not share any sides, and diagonal movement in the same direction goes through the corners at opposite ends of spaces.
Let me understand this correctly: A bishop on e8 moves in the direction of switch A4/a4. Further down in your description you say that in this case the bishop can only reach A4. But the bishop reaches the same corner of A4 and a4; therefore the bishop can decide whether to stop on A4 or a4.
So, in principle, a move into the switch, no matter from which direction and valid for all pieces, must result in a decision between the two squares of the switch - provided that the switch is not occupied.
My description for this is:
- Finally, you can move into a switch from below, from the side or from above. If the switch is not occupied, then you can choose whether the piece that moves into the switch is on 4 or a4 or 5 or h5 after the move. If the switch is occupied, then the piece in the switch must be captured; the opponent’s piece takes the place of the captured piece.
2. While some paths can lead to either Switch, others lead to only one space or the other in a Switch. For example, a Bishop on e8 can go to A4 or h5, and a Bishop on d1 can go to a4 or H5.
See the comments above.
A bishop on e8 or d1 can move to A4 or a4 respectively to h5 or H5.
Also, a Bishop on A4 can move away on either light or dark spaces, but one on a4 can move away only on light spaces.
But a bishop on A4 cannot move to f8. For that he would have to be on a4.
3. ... or one is occupied by an enemy piece. If a piece moves to the empty space in a Switch, and the other space is occupied by an enemy piece, that piece is considered captured.
A piece can only be captured on the square it stands. Therefore, in an occupied switch, you cannot move to the empty square and capture the piece on the other square of the switch. After the move into the occupied switch, the capturing piece stands on the square of the captured piece.
The Knight can leap directly to any space that could be reached in two one-space moves except for those reachable by two in the same direction.
I am not sure if the rule is correct. In my description I use a definition which comes from Alfred Pfeiffer (Chemnitzer Schachverband e.V.):
- The knight moves to one of the squares that a king can reach from the square in two moves, but which are not on the same row, line or diagonal. It does not move across squares that lie in between.
Let me understand this correctly: A bishop on e8 moves in the direction of switch A4/a4. Further down in your description you say that in this case the bishop can only reach A4.
Correct.
But the bishop reaches the same corner of A4 and a4; therefore the bishop can decide whether to stop on A4 or a4.
No, it cannot. Let me break the move down into steps. First, the Bishop on e8 moves to d7. At this point, movement in the same direction must go through the opposite corner is just passed through. This is the corner that d7 shares with c6. Continuing in the same direction, it can go to b5. At b5, it can move diagonally to A4, because b5 and A4 share a corner but no sides. Also, this is in the same direction that the move from e8 to b5 was in. However, b5 and a4 do share a side, which means that movement from one to the other is not diagonal. So, a move from e8 to a4 would be illegal.
So, in principle, a move into the switch, no matter from which direction and valid for all pieces, must result in a decision between the two squares of the switch - provided that the switch is not occupied.
No, that is completely the opposite of how I understand the rules.
A bishop on e8 or d1 can move to A4 or a4 respectively to h5 or H5.
This is unintelligible. If you mean what you said above, it is contrary to my understanding of the rules.
Also, a Bishop on A4 can move away on either light or dark spaces, but one on a4 can move away only on light spaces.
But a bishop on A4 cannot move to f8. For that he would have to be on a4.
That is correct, and I didn't say anything to the contrary. The light path from A4 goes through b3, c2, and d1.
- ... or one is occupied by an enemy piece. If a piece moves to the empty space in a Switch, and the other space is occupied by an enemy piece, that piece is considered captured.
A piece can only be captured on the square it stands. Therefore, in an occupied switch, you cannot move to the empty square and capture the piece on the other square of the switch. After the move into the occupied switch, the capturing piece stands on the square of the captured piece.
Are you saying that a piece cannot capture a piece in a Switch unless it can move to the space the piece is on? Or are you saying that when a piece can move to either space in a Switch, it can move to the Switch and capture the piece, and then it must occupy the space the piece was on?
The Knight can leap directly to any space that could be reached in two one-space moves except for those reachable by two in the same direction.
I am not sure if the rule is correct. In my description I use a definition which comes from Alfred Pfeiffer (Chemnitzer Schachverband e.V.):
- The knight moves to one of the squares that a king can reach from the square in two moves, but which are not on the same row, line or diagonal. It does not move across squares that lie in between.
They are the same, but I removed the ambiguities in his description and used some technical language. Since the King cannot move into check, and a Knight is not subject to the same restriction, I replaced the reference to two King moves with one to two one-space moves. Since I would normally refer to ranks and files rather than to rows and lines, and since I have been using these words in an algebraic sense rather than a geometric sense, I rewrote it to not use them. To "leap directly" is technical terminology that implies that a move "does not move across squares that lie in between."
No, it cannot. Let me break the move down into steps. First, the Bishop on e8 moves to d7. At this point, movement in the same direction must go through the opposite corner is just passed through. This is the corner that d7 shares with c6. Continuing in the same direction, it can go to b5. At b5, it can move diagonally to A4, because b5 and A4 share a corner but no sides. Also, this is in the same direction that the move from e8 to b5 was in. However, b5 and a4 do share a side, which means that movement from one to the other is not diagonal. So, a move from e8 to a4 would be illegal.
This is a very special consideration. Do you think that such can be communicated to potential players?
Why do we leave out consideration of equal/different corners and sides? Can't we agree that switches can be entered from all sides and a choice must be made between the fields of the switch? Surely that would be much easier for everyone.
In the discussion at the time, I just took your position, but ran into a wall looking for a simple solution. I came to the conclusion that switches have a special status, which must lead to a choice between the fields of a switch from all sides - from above, from below and from the side.
No, that is completely the opposite of how I understand the rules.
A bishop on e8 or d1 can move to A4 or a4 respectively to h5 or H5.
This is unintelligible. If you mean what you said above, it is contrary to my understanding of the rules.
What can I say? I think my position is quite logical. At the beginning of the discussions, I was of the opinion that switches work differently when they are operated from below, from the side, or from above. I have abandoned this opinion and changed it in favor of a pragmatic solution, in that a switch must be handled the same regardless of the direction.
Are you saying that a piece cannot capture a piece in a Switch unless it can move to the space the piece is on? Or are you saying that when a piece can move to either space in a Switch, it can move to the Switch and capture the piece, and then it must occupy the space the piece was on?
This seems to me to be much simpler than you make it out to be.
After all, a piece can only be captured where it is. Why should this be different for a switch?
Why should a piece be able to move to A4, and thereby capture a piece on a4 quasi en passent? That only happens with pawns. But that's where it should stay. The basic principle should be that pieces are captured on the square on which the pieces were placed. Pragmatic solution, isn't it?
They are the same, but I removed the ambiguities in his description and used some technical language. Since the King cannot move into check, and a Knight is not subject to the same restriction, I replaced the reference to two King moves with one to two one-space moves. Since I would normally refer to ranks and files rather than to rows and lines, and since I have been using these words in an algebraic sense rather than a geometric sense, I rewrote it to not use them. To "leap directly" is technical terminology that implies that a move "does not move across squares that lie in between."
I think I have understood that.
Why do we leave out consideration of equal/different corners and sides?
I have not done that. I consider equal ones equally and different ones differently, which is what makes most sense.
Can't we agree that switches can be entered from all sides and a choice must be made between the fields of the switch? Surely that would be much easier for everyone.
No, it would not be easier for everyone. This makes the game more confusing and complicated, because paths to and from Switch spaces are no longer symmetrical with each other. This would allow one King to attack another, and the following position would count as checkmate.
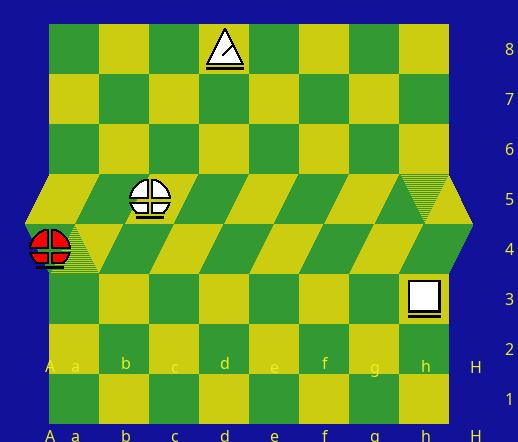
I think my position is quite logical.
It's not logical. At best, it is not outright contradictory.
At the beginning of the discussions, I was of the opinion that switches work differently when they are operated from below, from the side, or from above.
That's the position which makes the most sense, because it makes how Switches work a consequence of the geometry of the board.
I have abandoned this opinion and changed it in favor of a pragmatic solution, in that a switch must be handled the same regardless of the direction.
This conflicts with the rule that the space a piece is on in a Switch determines how it may move away. While you could have both rules, it makes the game more confusing.
Are you saying that a piece cannot capture a piece in a Switch unless it can move to the space the piece is on? Or are you saying that when a piece can move to either space in a Switch, it can move to the Switch and capture the piece, and then it must occupy the space the piece was on?
This seems to me to be much simpler than you make it out to be. After all, a piece can only be captured where it is. Why should this be different for a switch?
I was asking you to clarify which of two possible interpretations of what you said is the correct interpretation, but you didn't do that.
Why should a piece be able to move to A4, and thereby capture a piece on a4 quasi en passent? That only happens with pawns. But that's where it should stay. The basic principle should be that pieces are captured on the square on which the pieces were placed. Pragmatic solution, isn't it?
In both of the alternatives I asked you about, the capturing piece ends up on the space the captured piece was on. But you have not indicated which you have in mind. So, let me illustrate the difference.
In this position, can the Black Pawn capture the White Pawn and move to A4? Or is the Black Pawn unable to capture the White Pawn, because the move from c5 to A4 is not diagonal?
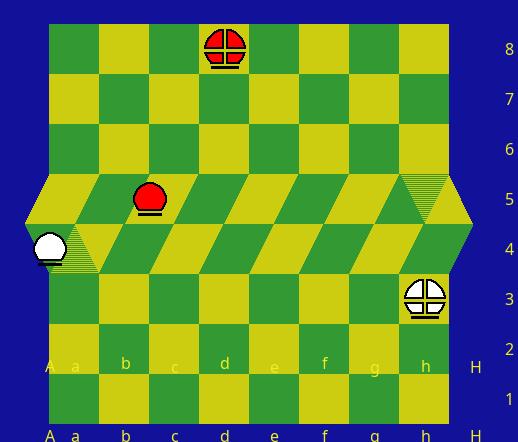
 Bn Em wrote on Sun, Nov 13, 2022 09:45 PM UTC in reply to Gerd Degens from Sat Nov 12 04:35 PM:
Bn Em wrote on Sun, Nov 13, 2022 09:45 PM UTC in reply to Gerd Degens from Sat Nov 12 04:35 PM:You can certainly scrap the entire concept.
I'm not sure which part of my comment you took as scrapping anything; certainly that was not the intent. Merely a minor note that your use of the word ‘maximum’ implied a liimitation I don't see
Mind games should be able to be discussed. Or do you have a different opinion?
I fully agree; if I differed in opinion there would be little reason for me continuing to frequent this forum. Did I imply something else?
At the beginning of the discussions, I was of the opinion that switches work differently when they are operated from below, from the side, or from above. I have abandoned this opinion and changed it in favor of a pragmatic solution, in that a switch must be handled the same regardless of the direction.
From what I remember, the discussion was limited specifically to movement via the side of a switch space: your original description allowed (rook) movement from A4 (using Fergus' notation) along the rank to e.g. b4, but not vice versa, breaking the usual assumption that slider moves are reversible. The ‘pragmatic solution’ you refer to was specifically to allow orthogonal slides from/via b4 to reach either of A4 or a4. It might be noted that disallowing all sideways movement from A4 would have achieved the same effect.
As far as I remember entry from the top of a switch, orthogonally or diagonally, was never controversial in this way, and as Fergus has noted unifying downward entry in the same way as for sideways entry leads to exactly the problem of asymmetry that unifying sideways entry was supposed to avoid.
...because paths to and from Switch spaces are no longer symmetrical with each other. This would allow one King to attack another, and the following position would count as checkmate.

I can't see anything other than a checkmate situation. The legal moves of the black king are vertically a5 and a3, horizontally b4 and diagonally b5 and b3. The move to c5 is excluded and only with that can the black king free itself.
We had such a situation in the discussion below and it involved a bishop on A4.
Also, a Bishop on A4 can move away on either light or dark spaces, but one on a4 can move away only on light spaces.
But a bishop on A4 cannot move to f8. For that he would have to be on a4.
That is correct, and I didn't say anything to the contrary. The light path from A4 goes through b3, c2, and d1.
If the bishop on A4 cannot move towards f8, then the king on A4 cannot move to c5? On the other hand, the white king can capture the black king on A4. This is undoubtedly an asymmetry that, as I understand it, cannot be avoided when handling a switch.

I guess I didn't understand your question correctly. I'll try my best to answer.
The switch is occupied, so the black pawn can move diagonally into the switch. In my opinion, the black pawn does not have a choice between A4 and a4, but moves directly to A4 and captures the white pawn there.
I took the discussion from earlier to heart and to that extent I thought about it and adjusted the rules. The result:
I find the idea that a bishop on d1 can only move to a4 or to H5, or a bishop on e8 can only move to A4 or h5, to be completely illogical.
You can bend it with corners and sides so that it seems logical, but basically, from my point of view, it leads to complicating the rules.
The rule that a switch is a place of decision to occupy the squares of a switch uniquely, no matter from which direction the switch is occupied, seems to be a clear rule that everyone can understand. I do not think that such a rule complicates the course of the game.
The concept implies that unsymmetrical move sequences cannot be excluded. I cannot express it in any other way.
I find the idea that a bishop on d1 can only move to a4 or to H5, or a bishop on e8 can only move to A4 or h5, to be completely illogical.
Assuming you mean the spaces in a Switch it can move to and not the full range of its movement, this logically follows from the geometry of the board.
You can bend it with corners and sides so that it seems logical, but basically, from my point of view, it leads to complicating the rules.
As an experienced programmer of Chess variants who has tried to program your game, I can give you my expert opinion that this is not true.
The rule that a switch is a place of decision to occupy the squares of a switch uniquely, no matter from which direction the switch is occupied, seems to be a clear rule that everyone can understand. I do not think that such a rule complicates the course of the game.
It really does complicate the course of the game. It is a tacked-on that does not follow from the geometry of the board, and the code required to enforce it would be more complex than the code required to enforce the rule you mistakenly imagine is illogical.
 Greg Strong wrote on Tue, Nov 15, 2022 01:45 AM UTC in reply to Fergus Duniho from 12:30 AM:
Greg Strong wrote on Tue, Nov 15, 2022 01:45 AM UTC in reply to Fergus Duniho from 12:30 AM:I have to agree with Fergus. You've created an interesting geometry, but then decided not to honor it.
 H. G. Muller wrote on Tue, Nov 15, 2022 08:01 AM UTC in reply to Greg Strong from 01:45 AM:
H. G. Muller wrote on Tue, Nov 15, 2022 08:01 AM UTC in reply to Greg Strong from 01:45 AM:Everything here seems to have been designed with the goal of confusing the player as much as possible as leading principle. The board is needlessly distorted, coordinates are needlessly garbled... It is also possible to to draw a regular 8x8 board such that all squares become diamonds, and files and ranks become spirals. Or to assign the rank labels a-h in the opposit direction on ranks 5-8.
I now understand that a bishop from d1 can only reach H5 - sometimes it takes a little longer, sorry. G4 shares a side with h5 and so a move to h5 is not diagonal. But why can't a bishop from d1 move to A4 and what am I still overlooking here? B3 shares neither a side with a4 nor with A4. In this respect, a move from b3 to a4 is just as diagonal as a move from b3 to A4. If A4 is not possible, then a color change of the bishop from d1 via A4 to e8 is also not possible. Only the color change from e8 via A4 to d1 would be possible. The situation with the switch h5/H5 applies vice versa. What do I not realize here?
Should the description consider the following knight moves?
Knight on b3, is the move to a5 possible, because on the same diagonal? Or a knight on a3, are the moves to a5 or b5 possible, because on the same line?
 Bn Em wrote on Tue, Nov 15, 2022 12:45 PM UTC in reply to Gerd Degens from 10:34 AM:
Bn Em wrote on Tue, Nov 15, 2022 12:45 PM UTC in reply to Gerd Degens from 10:34 AM:But why can't a bishop from d1 move to A4 and what am I still overlooking here?
It can; the discussion was whether a bishop can move from e8 could move onto both of a4 and A4, whereas it ought only to be able to move to A4; from f8 it could instead move to a4 but notA4`.
Should the description consider the following knight moves? Knight on b3, is the move to a5 possible, because on the same diagonal? Or a knight on a3, are the moves to a5 or b5 possible, because on the same line?
That depends on the definition of the Knight move: by the subtractive definition you and Fergus have used, those would be disallowed as a Queen could move to those spaces, as you've noted. Other definitions (such as the traditional ‘one orthogonal step then one step diagonally outward (or vice versa)’) would include those squares.
Which definition you prefer is in this case up to you
But why can't a bishop from d1 move to A4 and what am I still overlooking here?
It can move from d1 to A4. Here is a diagram I made for my Reroute66 page yesterday:

Should the description consider the following knight moves? Knight on b3, is the move to a5 possible, because on the same diagonal?
By your rules, I think it is not legal. By Reroute66 rules, it is legal, and I have illustrated it in a diagram on that page.
Or a knight on a3, are the moves to a5 or b5 possible, because on the same line?
I have also illustrated this on my Reroute66 page, because they are legal in that game.
Chess66 uses a different rule for Knight moves than Reroute66 does. Mine says that a Knight can leap directly to any non-adjacent space reachable by any combination of a single lateral and a single diagonal move. Your rule says that a Knight may leap two spaces away to any space not on the same line, row, or diagonal, which I assume are all meant in a geometric sense. While mine specifies the types of moves, yours does not, and it replaces this with a stricter restriction on which spaces a Knight may leap to. Besides excluding moves to non-adjacent spaces, it also excludes moves to spaces in the same row, line, or diagonal.
Since both rules would give you the Knight's usual moves on an 8x8 Chess board, this doesn't provide a basis for comparison. I favor the rule I use, because it allows the Knight to gain some additional powers of movement around a Switch. By making the Knight an inverse of the Queen, as your rule does, it weakens the Knight around the Switches, which I don't think is fair for what is already the weakest piece in the game.
Have read your explanations in Reroute66 and am now calmed down that from d1 a4 and A4 can be reached (was completely unsure for me before). In this respect, the color change of the bishop from d1 via A4 to e8 takes place (vice versa the situation from e8 to H5).
In the following constellation you show the possible moves of a knight in Reroute66.
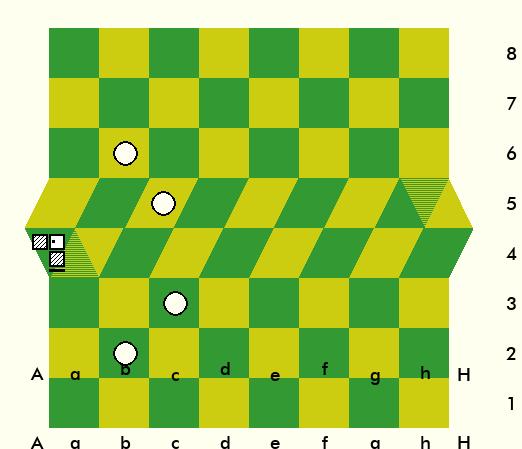
Is it possible that the move to d5 is missing here?
Is it possible that the move to d5 is missing here?
That move is illegal in Reroute66, for it cannot be reached by any combination of a lateral move and a diagonal move. Unlike Chess66, A4 and b4 are not laterally adjacent in Reroute66. They do share a corner, though. So, I'm wondering whether I should tweak my definition of diagonal to not count them as diagonally adjacent, or if I should say they are diagonally adjacent though they aren't part of a longer series of spaces diagonally connected in the same direction. If I go with the latter, the Knight could also move to c4, and a Bishop on A4 could also move to b4, though it couldn't go any further, because none of the diagonal directions on d4 would be in the same direction.
I guess I could say that two spaces are diagonally adjacent if they share nothing but a corner, and there is a straight path from approximately the center of one space to approximately the center of the other that passes only through that corner without passing through other spaces. For A4 and b4, the only straight path between their centers would go through a4
More simply, I might say that two spaces are diagonally adjacent if they share nothing but a corner, and there is a path between them that passes straight through that corner without touching their sides.
@H. G. Muller, I actually found this variant to be quite interesting to play, especially since the only difference here is the two modified rows and two additional fields, which affect the playing process dramatically enough without much change from the initial chess properties.
The definition of the Knight move is not correct. On an undistorted board it would allow the Knight to also move like Wazir or Ferz. This could be fixed by also excluding moves that are reachable in a single step.
I missed that before, but you are correct. I can rewrite it like this:
The Knight can leap directly to any space that could be reached in two one-space moves except for those reachable by a Rook or Bishop. Since it's a one-space move from A4 to b4 or from H5 to g5, a Knight on A4 or H5 can leap further away than a Knight can normally leap.
23 comments displayed
Permalink to the exact comments currently displayed.
If we're extrapolating already, why stop there? You could always get the 3rd and 6th ranks involved too, maybe even the 2nd and 7th if you don't mind the pawns starting on switches…
And/or you could have some more switches of the Chess 69 variety along the top and bottom if that's not enough strange topological shenanigans.